Advances in Regional Flood Frequency Analysis (RFFA)
 .
.
When flood frequencies are needed at an ungauged watershed, flow data from other watersheds are translated over based on watershed characteristics like shape and hydroclimate variables. This process is called RFFA, and takes machine learning to the next level, because we don’t need a “best guess” that typical machine learning algorithms produce – we need an entire predictive distribution that can be extrapolated to high quantiles.
This past spring, I spearheaded a 2-month project with four students from the University of British Columbia’s Master of Data Science program for their capstone project. We explored improvements to two RFFA approaches on watersheds in Canada: the index flood method and the direct quantile estimation method.
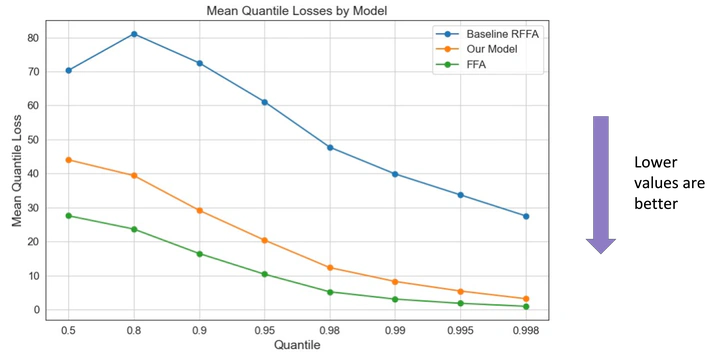
The index flood method assumes that the “flood ratios” of annual maximum flows to their watershed’s index flood (such as the mean or median) has the same distribution as flood ratios of similar watersheds. We found that a machine learning model estimated the index flood (mean log flow, in our case) better than a linear model did, especially when weighting the data to avoid preferential fitting to high or low flows. We also found that estimating the common distribution of flood ratios by pooling the flood ratios instead of averaging models watershed-by-watershed improved performance as well. Performance was ultimately evaluated using the mean quantile score (see the featured photo made by the students), which evaluates how good an estimate is at being a quantile. Another improvement for future research is to account for correlation between gauges when pooling the data (e.g., through a mixed effects model) so as to avoid potential bias that arises from pooling.
The direct quantile method relaxes the assumption of equal distributions of the flood ratios, so that each gauge is allowed to have its own distribution. This analysis is typically done by fitting a distribution to each gauged watershed deemed similar to the one of interest, and then fitting a linear regression to predict quantiles from watershed characteristics for each return period of interest. While advances here could not be fully fleshed out in the allotted time, we were able to bypass the need to estimate gauge-based quantiles, fitting a machine learning model to directly estimate quantiles from the raw data. This allows for more data to be used, coming from gauges with short records.